Index of /er21demo

	Name	Last modified	Size	Description
	Parent Directory		-
	ProductsDDI-phone.gel	2021-08-16 10:12	39K
	ProductsDDI-phone.png	2021-08-16 10:12	45K
	ProductsDDI.gel	2021-08-16 10:12	37K
	ProductsDDI.png	2021-08-16 10:12	17K
	ProductsMLT-phone.gel	2021-08-16 10:12	34K
	ProductsMLT-phone.png	2021-08-16 10:12	27K
	ProductsMLT.gel	2021-08-16 10:12	33K
	ProductsMLT.png	2021-08-16 10:12	20K
	SOURCES/	2021-08-17 10:22	-
	acrosslevels.gel	2021-08-16 10:12	27K
	acrosslevels.png	2021-08-16 10:12	31K
	cc-by-sa-4.0.txt	2021-08-16 10:12	20K
	partialevaluation-car.gel	2021-08-16 10:12	31K
	partialevaluation-car.png	2021-08-16 10:12	16K
	partialevaluation.gel	2021-08-16 10:12	31K
	partialevaluation.png	2021-08-16 10:12	58K

Download ConceptBase Φ Multi-Level Modeling Φ ConceptBase Team Φ Home

• Manfred Jeusfeld: Multilevel Modeling with ConceptBase. In: Proceedings of Demos and Posters Session at the 40th International Conference on Conceptual Modeling (ER 2021), CEUR Workshop Proceedings, Vol. 2958, 2021 (pdf).

This directory contains the ConceptBase/Telos sources models for the above paper plus instructions to run the demo on your own computer and links to videos of the demonstration. Further information on multilevel modeling with ConceptBase is also available at http://conceptbase.sourceforge.net/CB-MLM.html.

The source models (*.sml, *.sml.txt,*.cbs) in this directory (incl. subdirectories) and their derivates (*.gel,*.png) are provided under a CC BY-SA 4.0 license: Attribution-ShareAlike 4.0 International.

Installation

• Use your Web browser (e.g. Firefox) to click on a link to a graph file like acrosslevels.gel. The browser shall ask you whether to download the file or associate an application. Choose to associate an application. Then, browse to the installation directory of ConceptBase.cc (Windows: c:\conceptbase, other: $HOME/conceptbase). Type for Windows "cbgraph.bat" and for other platforms "cbgraph" in the filename field and press OK. Afterwards, a click on a link to a graph file shall directly start CBGraph. Our web servers of ConceptBase use as Mime type for graph files application/cbgraphfile or application/x-cbgraphfile. The latter is preferred.

Part 01: Introduction to metamodeling with ConceptBase

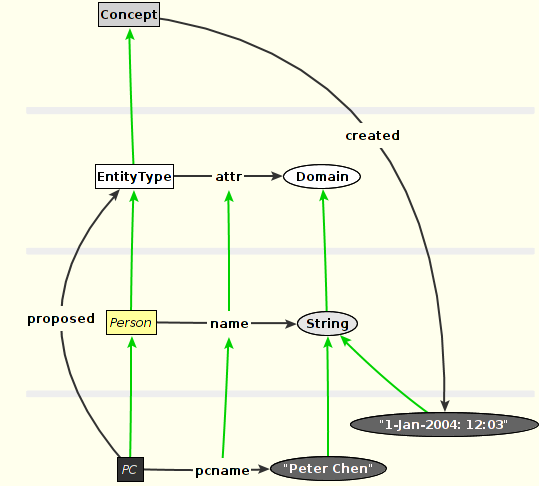
In this part, we shortly introduce the main constructs of Telos, the data model underlying ConceptBase. In short, Telos allows arbitrarily high instantiation hierarchies. Generic constructs (instantiation, specialization, attribution) are defined with the so-called "omega" class Proposition. Any explicit information is an instance of the omega class Proposition (other frameworks use the term "Object" for such a class).

Click on the image icon on the right to start CBGraph with the "acrosslevels" example. Note that there are some attribution facts such as (PC proposed EntityType) that span instantiation levels. The "attribute" link of Proposition serves both for attributes and relations. This sets Telos apart from other conceptual modeling languages. However, you can well define your own link type to distinguish attributes and relations.

The green broken links are instantiation relations. In the demo, we shall show that the nodes and links on the right side are all instance of the omega class Proposition. This unique property of Proposition is later exploited for defining MLT-Telos as an extension of Telos.

Video Part 01: Metamodeling with ConceptBase

Part 02: Multilevel modeling with Dual Deep Instantiation (DDI)

Dual deep instantiation was our first attempt to realize multilevel modeling with ConceptBase. All constructs of DDI were defined within Telos using about 30 rules and constraints. The technical details are reported at http://conceptbase.sourceforge.net/ddi/. In the demonstration, we show how the objects, classes, and metaclasses are defined in the DDI extension of Telos, and how potencies are assigned to multilevel attributes/relations in DDI.

We also have a short look at the rules and constraints defining the constructs of DDI. DDI is based on potency numbers assigned to attrubutes/relations. The rules and constraints govern how the potencies are decremented when defining attributes/relations at instances. DDI uses its own omega class "OBJECT" and also defines instantiation, specialization and attribution independently from the counterparts of Telos. Telos/ConceptBase is merely used as the implementation platform. The existing Telos axioms for instantiation, specialization and attribution are only used for representational purposes, not for simplifying the axioms needed for DDI instantiation, specialization and attribution. Still, DDI is more expressive than the MLT-Telos approach discussed in the next part. It allows to constrain multilevel attributes/relations at lower abstraction levels (also for subclasses). From the viewpoint of the rule/constraint language of ConceptBase, DDI was a challenging exercise since ConceptBase virtually only supports binary predicates. Functiond and parameterized query classes had to be used to cover the more complex notions of DDI, such as finding out which constraints on an attribute are applicable when many classes define an attribute with a given label.

Video Part 02: Dual Deep Instantiation

Part 03: Multilevel modeling with MLT-Telos

MLT-Telos is based on the powertypes to realize multilevel modeling. Unlike DDI, it reuses the semantics of instantiation, specialization and attribution that come with Telos. This greatly reduces the number of axioms.

The levels/potency numbers used in DDI are replaces by chains of "powertype" relations. For example, the class ProductType is a metaclass (abstraction level 2). It is the powertype of the class Product, which is a simple class (level 1). All instances of ProductType (like Car) are subclasses of Product. So, all instances of Car can "see" all attribute definitions of Product. You should consider the classes of a powertype chain as one complex object. The attributes/relations are defined at one level above where they are going to be used.

More details on MLT-Telos are provided at http://conceptbase.sourceforge.net/mlt-telos/. While DDI allows to define an attribute/relation at many places in the class hierarchy, MLT-Telos only supports to define it at a single abstraction level.

Video Part 03: MLT-Telos

Part 04: Partial evaluation of multilevel rules

Both DDI and MLT-Telos rely heavily on the metamodeling and logic-based capabilities of ConceptBase. Of particular interest may be how the partial evaluation of multilevel rules can be used to generate much more efficient rule sets. ConceptBase will translate only so-called multilevel rule or constraint to a set of two-level rules/constraints. Those partially evaluated rules and constraints have less variables and are this more efficient to evaluate by the Datalog engine of ConceptBase. Further, it makes sure that an instantiation predicate (x in c) only has constants in the class position "c".

More information on partial evaluation in ConceptBase is available at http://conceptbase.sourceforge.net/link-semantics.html and in the ConceptBase user manual, see section of "Meta formulas".

Video Part 04: Partial Evaluation

Note: The video uses a graph view showing a link (Car specializes Product). The multilevel formula however displays a predicate (t1 specializes_1 t2). We changed the graph file on this page to show the link (Car specializes_1 Product). Both are correct, since the "specializes" predicate is the transitive closure of the "spezializes_1" via a deductive rule in the definition of MLT-Telos.