
DeepTelos2 Φ Download Φ Forum Φ Team Φ Home
The latest greatest version of DeepTelos is found here: DeepTelos2. It supports all functions of the original DeepTelos (described below) plus a better integration with the Telos specialization. All versions of Telos are defined by a small set of rules and constraint that you can add to your ConceptBase model.
This directory contains the implementation and examples for the paper
Manfred A. Jeusfeld, Bernd Neumayr: DeepTelos: Multi-level Modeling with Most General Instances. In Proc. 35th International Conference on Conceptual Modeling (ER 2016), Gifu, Japan, Springer, LNCS 9974, 2016, pp. 198-211 (slides@ER'2016 by Bernd).The source models (*.sml.txt,*.cbs) in this directory (see directory listing at the bottom of this page) and their derivates (*.gel,*.png) are provided under a CC BY-NC 4.0 license: Attribution-NonCommercial 4.0 International. You need ConceptBase 7.8 released July 2016 or later to test the implementation. Download it from http://conceptbase.cc.
You can configure your ConceptBase installation to directly start the example graph files (*.gel). The graph files contain all necessary Telos definitions including the DeepTelos axioms and the dedicated graphical types. You only need to configure your web browser to open the CBGraph utility when you click a graph file. The procedure is simple:
DeepTelos is an extension of Telos by three additional axioms that define multi-level modeling. A new construct "most general instance" (predicate "IN") allows to define multiple hierarchies of levels into which instances are classified. This allows to define properties and relations at various abstraction levels.
There are two revisions Rev 1 and Rev 2 of DeepTelos that allow
to use the inheritance principle in the upward and downward directions. We recommend to use the latest
revision.
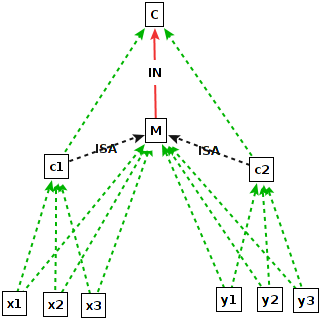
 The generic example defines the most general instance M of a class C.
The class C has two instances c1 and c2.
These instances have themselves instances x1, x2, x3 and y1, y2, y3, respectively.
This information is explicitely defined. This is shown in the first screendump deeptelos0a.png.
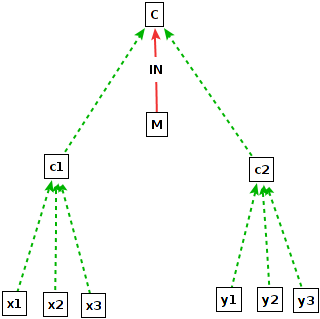
The second screendump deeptelos0.png shows in addition the information derived by the DeepTelos axioms.
The first DeepTelos axiom 'mrule1' is:
The generic example defines the most general instance M of a class C.
The class C has two instances c1 and c2.
These instances have themselves instances x1, x2, x3 and y1, y2, y3, respectively.
This information is explicitely defined. This is shown in the first screendump deeptelos0a.png.
The second screendump deeptelos0.png shows in addition the information derived by the DeepTelos axioms.
The first DeepTelos axiom 'mrule1' is:
forall m,x,c/Proposition (x in c) and (m IN c) ==> (x ISA m)In our example, it derives the facts (c1 ISA M) and (c2 ISA M). The second DeepTelos axiom 'mrule2' is:
forall x,c,d/Proposition (c ISA d) and (x in c) ==> (x in d)This is the classical class membership inheritance for specializations. This rule then populates the class M with all instances of its subclasses c1 and c2, i.e. x1, x2, x3, y1, y2, and y3. Thus, M is populated with all instances of all instances of C. This instantiation to M allows to define attributes/relations at M that are applicable to all its (derived) instances. The class M is essentially a proxy of class C at one abstraction level lower. While C has instances like c and d, the class M has the instances of c and d as instances. It is called the "most general instance" of C because it is the superclass of all instances of C. In the example, the class M defines a relation 'a' to class d. Since x1 is a derived instance of M, it can instantiate this relation.
 The first example features a simple product hierachy Product-ProductModel-ProductCategory.
A sibling hierarchy CarModel-Car is defined as specialization of ProductModel.
Car and Product are simple classes (OMG M1 level). CarModel and Car are meta classes (M2)
and ProductCategory is a metameta class (M3). The DeepTelos axioms make sure that all
cars are instances of Car and all products are instances of Product. Likewise, all
car models will be instances of CarModel and all product models (incl. all car models)
are instances of ProductModel.
The first example features a simple product hierachy Product-ProductModel-ProductCategory.
A sibling hierarchy CarModel-Car is defined as specialization of ProductModel.
Car and Product are simple classes (OMG M1 level). CarModel and Car are meta classes (M2)
and ProductCategory is a metameta class (M3). The DeepTelos axioms make sure that all
cars are instances of Car and all products are instances of Product. Likewise, all
car models will be instances of CarModel and all product models (incl. all car models)
are instances of ProductModel.
 This example puts the (ontological) product hierarchy next to the (lingustic) Entity-EntityType hierarchy.
So, products also are entities.
This example puts the (ontological) product hierarchy next to the (lingustic) Entity-EntityType hierarchy.
So, products also are entities.

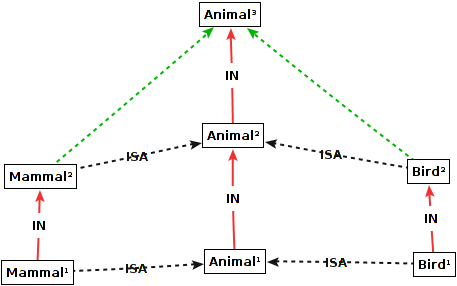 Animal species are organized in taxonomies for mammals, birds, fishes etc. In this example,
we use superscripts to express the hierarchy levels. Hence, Animal1 stands for
all physical animals. It is the most general instance of Animal2, which stands
for animal species such as 'Dog' and 'Chicken'. Finally, Animal3 is the class
of animal categories such as mammals, birds etc. Those categories get their taxonomies as well
to classify for example all physical mammals (e.g., 'pluto' being a dog and thus a mammal).
Animal species are organized in taxonomies for mammals, birds, fishes etc. In this example,
we use superscripts to express the hierarchy levels. Hence, Animal1 stands for
all physical animals. It is the most general instance of Animal2, which stands
for animal species such as 'Dog' and 'Chicken'. Finally, Animal3 is the class
of animal categories such as mammals, birds etc. Those categories get their taxonomies as well
to classify for example all physical mammals (e.g., 'pluto' being a dog and thus a mammal).
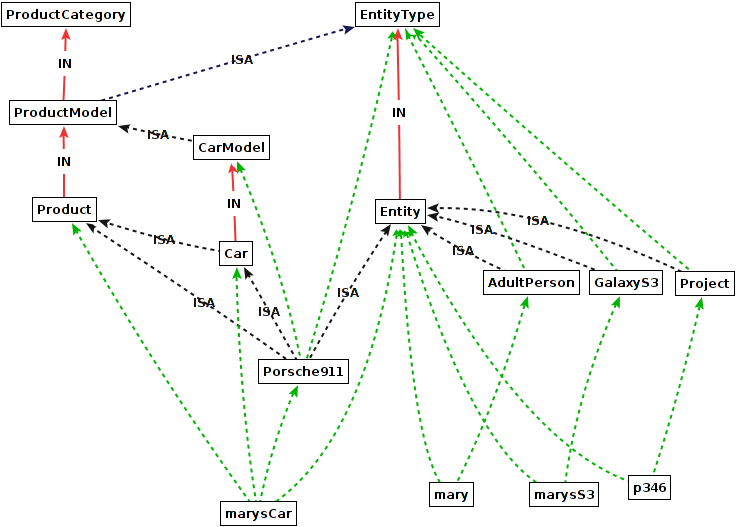 In example 2, the class Porsche911 was defined as instance of EntityType. In this variant,
we define ProductModel as specialization of EntityType. This will
ensure that any instance of ProductModel (incl. Porsche911) also is an instance of EntityType.
In example 2, the class Porsche911 was defined as instance of EntityType. In this variant,
we define ProductModel as specialization of EntityType. This will
ensure that any instance of ProductModel (incl. Porsche911) also is an instance of EntityType.
 Roll-up hierarchies are known from multi-dimensional data model. The classifical example is
time, e.g. the calendar of days rolled up to the parallel sub-hierarchies of calendar weeks
and calendar months.
Roll-up hierarchies are known from multi-dimensional data model. The classifical example is
time, e.g. the calendar of days rolled up to the parallel sub-hierarchies of calendar weeks
and calendar months.
 Telos regards attributes and relationships as first-class objects. This allows to apply
the construct of most-general instances to them as well. For example, the meta-class
EntityType defines an attribute 'property' to the meta-class Domain.
Entity is the most general instance of EntityType and Value is the most general instance
of Domain. Then, the attribute 'value' of Entity is defined as most general instance of
the 'property' attribute of EntityType.
Telos regards attributes and relationships as first-class objects. This allows to apply
the construct of most-general instances to them as well. For example, the meta-class
EntityType defines an attribute 'property' to the meta-class Domain.
Entity is the most general instance of EntityType and Value is the most general instance
of Domain. Then, the attribute 'value' of Entity is defined as most general instance of
the 'property' attribute of EntityType.
 Consider as example the 'budget' attribute of the entity type 'Project'. It is an instance of
the 'property' attribute of EntityType. Since the 'value' attribute is its most general instance,
all attributes like 'budget' become a specialization of the 'value' attribute.
The example project 'p346' has such a filler for the 'budget' property. Thus, it also becomes
an instance of the 'value' attribute of Entity.
The consequence is that we can now realize schema-less querying. For example, we can list all
entities that have a real number as value. Like 'value' is the most general instance of
'property', one can also define most general instances for the 'key' property of EntityType.
This will allow to formulate queries like for listing all entities that include foreign keys
of other entities.
Consider as example the 'budget' attribute of the entity type 'Project'. It is an instance of
the 'property' attribute of EntityType. Since the 'value' attribute is its most general instance,
all attributes like 'budget' become a specialization of the 'value' attribute.
The example project 'p346' has such a filler for the 'budget' property. Thus, it also becomes
an instance of the 'value' attribute of Entity.
The consequence is that we can now realize schema-less querying. For example, we can list all
entities that have a real number as value. Like 'value' is the most general instance of
'property', one can also define most general instances for the 'key' property of EntityType.
This will allow to formulate queries like for listing all entities that include foreign keys
of other entities.

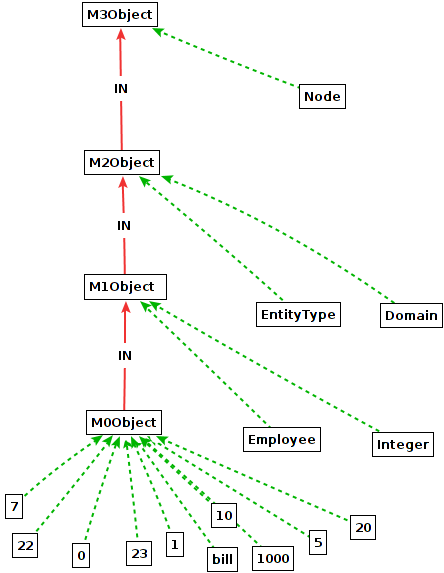 Telos was one of the first data models that fully supported objects at all abstractions levels:
proper objects (M0), simple classes (M1), metaclasses (M2), metametaclases (M3), and beyond.
The construct of most general instances can be used to define the semantics of these levels
by just three statements: (M0Object IN M1Object), (M1Object IN M1Object),
(M2Object IN M3Object). The axioms for DeepTelos then populate the classes by their
semantics: M0Object shall have all regular objects as instances,
M1Object has all simple as instances, and M1Object has all
metaclasses as instances.
Telos was one of the first data models that fully supported objects at all abstractions levels:
proper objects (M0), simple classes (M1), metaclasses (M2), metametaclases (M3), and beyond.
The construct of most general instances can be used to define the semantics of these levels
by just three statements: (M0Object IN M1Object), (M1Object IN M1Object),
(M2Object IN M3Object). The axioms for DeepTelos then populate the classes by their
semantics: M0Object shall have all regular objects as instances,
M1Object has all simple as instances, and M1Object has all
metaclasses as instances.
mrule2: $ forall x,c,d/Proposition (c ISA d) and (x in c) ==> (x in d) $
The diagram also shows the cascading effect of the DeepTelos axioms: the class Node is an instance of M3Object. Since M2Object is a most general instance of M3Object, the class Node become a subclass ("ISA") of M2Object. EntityType and Domain are instance of Node. Hence, the are also instances of M2Object. Now, since M1Object is a most general instance of M2Object, both EntityType and Domain become subclasses ("ISA") of M1Object. Next, Employee is declared an instance of EntityType, thus also an instance of M1Object. Since M0Object is a most general instance of M2Object, Employee (and analogously Integer) becomes a subclass ("ISA) of M0Object. Finally, any instance of Employee and Integer become instances of M0Object via inheritance.
The three facts (M2Object IN M3Object), (M1Object IN M2Object), (M0Object IN M1Object) are all that is needed to populate these level objects. Instances of M3Object will lead to specializations of the most general instance M2Object and thus instantiate all M2-level objects to M2Object. This instantiation then will populate M1Object, which finally ensures that M0Object is populated by all M0-level objects.
The number of derived specializations (x ISA m) is exactly the number of instances
of the class c in (m IN c). This number typically increases exponentially by descending the
level objects M3Object, ..., M0Object.
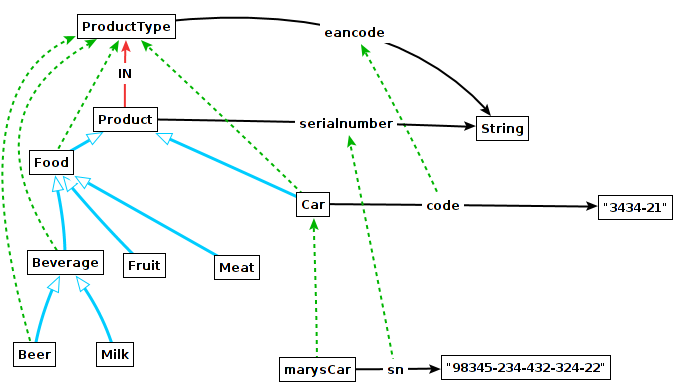
The original DeepTelos derives the specialization predicate (x ISA m) whenever (m IN c) and (x in c) is true. By this, m becomes the most general instance of the class c. This works fine when the modelling is done by instantiating the class c. It does not work, when the user rather prefers to define subclasses of m directly. This is done in ConceptBase by using the predefined predicate (x isA m).
To allow this second way of modeling, we modify mrule1 and add mrule4:
Proposition with
attribute
ISA: Proposition;
IN: Proposition
end
DeepTelosRules in Class with
rule
mrule1: $ forall m,x,c/Proposition
(x in c) and (m IN c) and not (x isA m) ==> (x ISA m) $;
mrule2: $ forall x,c,d/Proposition (c ISA d) and (x in c)
==> (x in d) $;
mrule3: $ forall c,d,m,n/Proposition
(m IN c) and (n IN d) and (c ISA d) ==> (m ISA n) $;
mrule4: $ forall m,x,c/Proposition
(m IN c) and (x isA m) ==> (x in c) $
end
The additional condition not (x isA m) in mrule1 makes sure that no redundant rules for specialization are generated. Note that both (x isA y) and (x ISA y) have virtually the same semantics. The noteworthy difference is that (x isA y) cannot be defined by user-defined deductive rules. So, the predicate (x isA y) is used for defining explicit specilization hierarchies.
The rule mrule 4 derives the instantiaton (x in c) from all (explicit) subclasses of its most-general instance m. It is like exchanging the position of (x ISA/isA m) with (x in c).
In the example, (Car in ProductType) is derived via mrule4 from the facts
(Product IN ProductType) and (Car isA Product).
In the original version of DeepTelos, one would define the facts
(Product IN ProductType) and (Car in ProductType)
to derive (Car ISA Product) via mrule1.
Both rules mrule1 and mrule4 co-exist, i.e. one can use most-general instances
on both ways and also mix both ways.
 Revision 2 supports specializing most-general instances
by allowing to mix the use of Telos-IsA and DeepTelos-ISA via mrule4 and mrule5.
The predicate :(x isA mx): returns explicit Telos-IsA subclasses of mx.
The constraint mconstr1 forbids cyclic instantiations between a most-general instance and
its class.
Revision 2 supports specializing most-general instances
by allowing to mix the use of Telos-IsA and DeepTelos-ISA via mrule4 and mrule5.
The predicate :(x isA mx): returns explicit Telos-IsA subclasses of mx.
The constraint mconstr1 forbids cyclic instantiations between a most-general instance and
its class.
Proposition with
attribute
ISA: Proposition;
IN: Proposition
end
DeepTelosRules in Class with
rule
mrule1: $ forall m,x,c/Proposition (x in c) and (m IN c) and not (x isA m) ==> (x ISA m) $;
mrule2: $ forall x,c,d/Proposition (c ISA d) and (x in c) ==> (x in d) $;
mrule3: $ forall c,d,m,n/Proposition (m IN c) and (n IN d) and (c ISA d) ==> (m ISA n) $;
mrule4 : $ forall m,x,c/Proposition (m IN c) and (x isA m) and not (x in QueryClass) ==> (x in c) $;
mrule5 : $ forall m,mx,x,c/Proposition (m IN c) and :(x isA mx): and (mx ISA m) and not (x in QueryClass) ==> (x in c) $
constraint
mconstr1: $ forall x,m,c/Proposition (m IN c) and (x in c) ==> not (x in m) $
end
In the example, the class GolderRetriever is declared as an explicit specialization
(blue specialization links = Telos-IsA) of Dog.
The rules mrule4 and mrule5 then make sure that GolderRetriever
is also an instance of Animal2 and Mammal2.
As a consequence, GolderRetriever becomes a subclass
(blue broken specialization links = DeepTelos-ISA) of Animal1 and MammalConsider for example deeptelos-principle.cbs in the section "The semantics of most general instances". The class C has two instances: (c1 in C) and (c2 in C). Further, it has the most general instance M: (M IN C). The first axiom of DeepTelos then derives two specializations: (c1 ISA M) and (c2 ISA M).
The second axiom of DeepTelos realizes the classical class membership inheritance for (c ISA d):
mrule2: $ forall x,c,d/Proposition (c ISA d) and (x in c) ==> (x in d) $This formula is subject to partial evaluation since both c and d are variables. ConceptBase uses the predicate (c ISA d) in the formula to compute all possible value combination for the two variables, in this case (c1 ISA M) and (c2 ISA M). The compilation then yields two partially evaluated formulas where the predicate (c ISA d) vanished by binding the variables to the constants in the facts (c1 ISA M) and (c2 ISA M). The resulting simplified formulas are added to the definition of M:
M in Class with
IN
class : C
rule
mrule2_generated : $ forall x/c1 (x in M) $;
mrule21_generated : $ forall x/c2 (x in M) $
end
The generated rules are structurally very simple: they copy the instances of the class c1 and c2
to the class M (=most general instance of C).
As a result, ConceptBase can very quickly compute the instances of class M.
The benefit of the partial evaluation further increases with hierarchies of most general instances.
Note that the clause x/c1 is a shortcut for (x in c1).
Another beneficial implementation feature of ConceptBase is the "tabling" used by ConceptBase to store the extension of derived predicates, such as (x in c). The extension is only computed once and only when needed, and then stored in an indexed data structure. If a class C with a most general instance M has many instances, then many rules like mrule2_generated are created. This could be in the thousands, if the class C has thousands of instances. This can lead to a huge extension of a class like M, which also is time-consuming to compute. The "tabling" feature of ConceptBase will however store the extension and speed-up subsequent accesses.
The class membership axiom mrule2 is formulated for the DeepTelos predicate (c ISA d) This predicate mimics the semantics of the original Telos predicate (c isA d), which is defined by a very similar axiom. For historical reasons, the Telos axioms in ConceptBase are hard-coded and not subject to partial evaluation. Still, it would have been preferable to use (c isA d) instead of (c ISA d). The technical reason that prevented its use is a restriction on the use of (c isA d) in rules: it may not occur as conclusion predicate. This restriction made good sense at the time when the Telos axioms were implemented in ConceptBase. It allowed to precompute the set of instances of superclasses in the object store. This optimization became virtually obsolete when tabling was introduced to implement recursive deductive rules. However, the technical restriction remains intact and forced us to define a second specialization predicate (c ISA d).
The original Telos axioms are hard-coded. They were meant to form the second stratum of predicates In(x,c), Isa(c,d), AL(x,m,n,y), and A(x,m,y). The first stratum is formed by the P-facts P(o,x,n,y). Certain axioms of Telos, in particular the attribute typing axiom, do in principle not "see" instantiation facts derived by user-defined rules such as mrule2. That would mean that DeepTelos databases would systematically violate the attribute typing axiom, whenever it is used to define attribute at most-general instances. The formal strata of Telos axioms have however been abandoned since several years in ConceptBase. In particular, the attribute typing axiom now also "sees" instances derived by user-defined rules.
| Name | Last modified | Size | Description | |
|---|---|---|---|---|
| Parent Directory | - | |||
| deeptelos-GTs.sml.txt | 23-Mar-2018 10:07 | 3.0K | ||
| deeptelos-level-containers.gel | 23-Mar-2018 10:04 | 19K | ||
| deeptelos-principle.cbs | 23-Mar-2018 10:05 | 1.1K | ||
| deeptelos-products-entities.cbs | 23-Mar-2018 10:05 | 2.8K | ||
| deeptelos-products-entities2.cbs | 23-Mar-2018 10:05 | 2.9K | ||
| deeptelos-products.cbs | 23-Mar-2018 10:05 | 2.2K | ||
| deeptelos-species.cbs | 23-Mar-2018 10:05 | 2.6K | ||
| deeptelos-telos.cbs | 23-Mar-2018 10:05 | 2.0K | ||
| deeptelos-time.cbs | 23-Mar-2018 10:05 | 2.1K | ||
| deeptelos.sml.txt | 23-Mar-2018 10:07 | 1.4K | ||
| deeptelos0.gel | 23-Mar-2018 10:04 | 10K | ||
| deeptelos0.png | 19-Aug-2016 11:58 | 13K | ||
| deeptelos0a.gel | 23-Mar-2018 10:04 | 9.7K | ||
| deeptelos0a.png | 19-Aug-2016 11:58 | 8.0K | ||
| deeptelos0b.gel | 23-Mar-2018 10:04 | 9.5K | ||
| deeptelos0b.png | 19-Aug-2016 11:58 | 7.1K | ||
| deeptelos1.gel | 23-Mar-2018 10:04 | 11K | ||
| deeptelos1.png | 16-Aug-2016 13:08 | 22K | ||
| deeptelos2.gel | 23-Mar-2018 10:04 | 12K | ||
| deeptelos2.png | 22-Aug-2016 09:54 | 25K | ||
| deeptelos3.gel | 23-Mar-2018 10:04 | 13K | ||
| deeptelos3.png | 22-Sep-2016 07:14 | 24K | ||
| deeptelos3a.gel | 23-Mar-2018 10:04 | 12K | ||
| deeptelos3a.png | 22-Sep-2016 07:14 | 11K | ||
| deeptelos4.gel | 23-Mar-2018 10:04 | 13K | ||
| deeptelos4.png | 16-Sep-2016 11:12 | 44K | ||
| deeptelos5.gel | 23-Mar-2018 10:04 | 12K | ||
| deeptelos5.png | 18-Aug-2016 09:54 | 49K | ||
| deeptelos6.gel | 23-Mar-2018 10:04 | 12K | ||
| deeptelos6.png | 23-Sep-2016 11:00 | 13K | ||
| deeptelos6a.gel | 23-Mar-2018 10:04 | 11K | ||
| deeptelos6a.png | 23-Sep-2016 11:12 | 11K | ||
| deeptelos7.gel | 23-Mar-2018 10:04 | 12K | ||
| deeptelos7.png | 04-Oct-2016 07:32 | 22K | ||
| deeptelos7a.gel | 23-Mar-2018 10:04 | 12K | ||
| deeptelos7a.png | 09-Jan-2017 10:52 | 22K | ||
| deeptelos8.gel | 23-Mar-2018 10:04 | 11K | ||
| deeptelos8.png | 13-Nov-2017 14:09 | 24K | ||
| deeptelos9.gel | 23-Mar-2018 10:05 | 9.7K | ||
| deeptelos10.gel | 23-Mar-2018 10:04 | 9.1K | ||
| deeptelos_r1.sml.txt | 23-Mar-2018 10:07 | 1.6K | ||
| deeptelos_r2-GTs.sml.txt | 23-Mar-2018 10:07 | 7.3K | ||
| deeptelos_r2-species.cbs | 23-Mar-2018 10:05 | 2.6K | ||
| deeptelos_r2.sml.txt | 23-Mar-2018 10:07 | 2.1K | ||
| jeusfeld-neumayr-deeptelos-final.pdf | 16-Nov-2016 10:56 | 1.0M | ||
| mammal-deeptelos_r2.gel | 28-Mar-2018 11:20 | 20K | ||
| mammal-deeptelos_r2.png | 28-Mar-2018 11:20 | 19K | ||