Download Φ License Φ Forum Φ Team Φ Home

Defining Semantics of Link Types with ConceptBase

ConceptBase's capabilities as a modeling tool can be extended by meta classes. The semantics of these meta classes, in particular the semantics of the link types defined for meta classes can be expressed by rules and constraints. Simply by using the link types in some class definition, the semantics is enacted.

Properties like transitivity, symmetry, reflexivity and others can be expressed by meta-formulas. An example is the following definition of transitivity and asymmetry:

Proposition in Class with
  attribute
     transitive: Proposition;
     asymmetric: Proposition
  rule
     trans_R: 
     $ forall x,y,z,M/VAR 
          AC/Proposition!transitive 
          C/Proposition
           P(AC,C,M,C) and (x in C) and 
           (y in C) and (z in C) and
           (x M y) and (y M z) ==> (x M z) $
  constraint
     asym_IC: 
     $ forall x,y,M/VAR
              AC/Proposition!asymmetric 
              C/Proposition
                P(AC,C,M,C) and (x in C) and 
                 (y in C) and 
                 (x M y)  ==> not (y M x) $
end

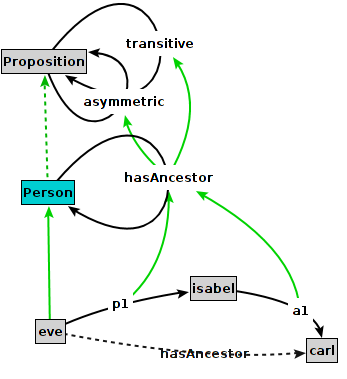
The link types are defined as attributes of the pre-defined class Proposition. The class Proposition has all objects as instances, including attributes of objects, specialization links (isA) and instantiation links (in). Hence, the link types are made available for any kind of object that is expressible in ConceptBase. The last line of the first formula is the well-known pattern of transitivity. The preceding lines are declaring the ranges of variables. Note that the formula ranges over classes C which define some attribute AC with label M which is defined as an instance of the transitive category. The definition of asymmetry is similar. The complete specification is available from the CB-Forum.

With these definitions, any class can use the link types simply by declaring the user-defined attribute as instance of the link type. For example, the hasAncestor relation of Person is both asymmetric and transitive:

Person in Proposition with
  asymmetric,transitive
     hasAncestor: Person
end

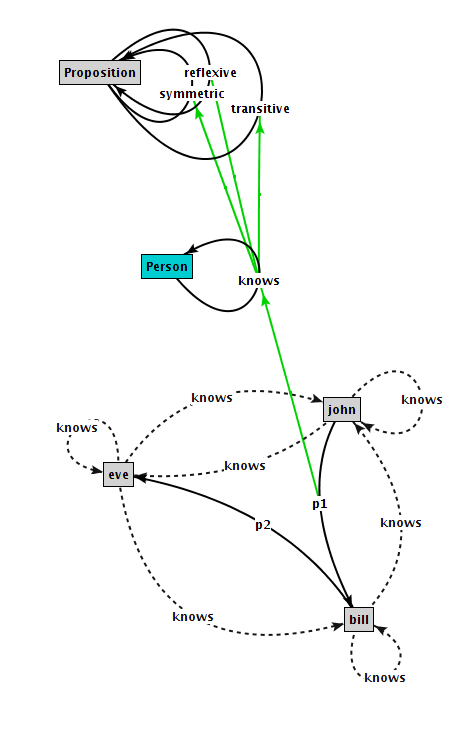
Using the same set of metaformulas, you can define an the knows attribute of Person.

Person with  
  reflexive,symmetric,transitive
    knows : Person
end

   forall x/Person (x knows x)
   forall x,y/Person (x knows y) ==> (y knows x)
   forall x,y,z/Person (x knows y) and (y knows z) ==> (x knows z)

http://conceptbase.cc -- Contact: M. Jeusfeld, University of Skövde, Box 408, S-54128 Skövde, Sweden
2014-04-14/M.Jeusfeld